Ecological Rationality of Demand Chasing

Posted on Tue 06 May 2014 in Core OM and supply chain

Experimental literature that has looked at newsvendor decision-making documents a phenomenon called demand chasing wherein a decision-maker adjusts her order quantity in each period toward the demand realization in past period. This behavior is so obviously “irrational” (given the typical newsvendor setup where each period’s demand is statistically independent of past demands) that operations literature has not had many reasons to comment on this, other than to simply document it as an error. This short article questions this conclusions that demand chasing is in fact an “error” to be overcome, and proposes that the behavior is in fact reasonable (and performs better compared to even the “optimal” behavior) in real-life settings. Thus, I argue the demand-chasing behavior emerges because of the disconnect between the artifical in setting stylized newsvendor model that is tested and the real-life inventory management tasks that managers face.

While theoretically possible, I am not sure that many demand time series would exhibit zero autocorrelation. For instance, even in the fashion industry, it appears plausible that demand depends on factors such as the store’s brand image, the buyer’s expertise, customer’s wealth, among others, all of which possibly exhibit positive autocorrelation. Hence, I argue that in many, if not all, real-life contexts, current demand does have predictive power for future demand and that in such scenarios with autocorrelated demands, I demonstrate through a formal model that the optimal newsvendor should indeed exhibit demand chasing behavior.

I illustrate the ecologically rationality of demand-chasing by considering a more realistic AR(1) demand process and assessing the performance of pure demand-chasing versus the performance of “optimal” newsvendor quantities that fails to account for the autocorrelation structure of the demand process. my results demonstrate that a demand-chasing manager who is “irrational” that she does not even employ the prices or margins in their optimization can perform better relative a manager who makes the “optimal” newsvendor decision while neglecting the autocorrelation structure of demand. Thus, I argue that demand-chasing is not an bug to be fixed, but is a feature of an ecologically rational ordering process suited to realistic demand processes that managers have prior experience with (and will probably face in the future).

Model & Analysis

The basic structure I consider is the canonical newsvendor model. Specifically, I consider a manager who is required to place order $Q_{t}$ in period $t$. I assume that the cost per unit is $c$, and that the price at which she can sell it (conditional on there being demand for the product) is $p$. To keep matters simple, I shall assume that there is no salvage value for any left over inventory and that, as in typical newsvendor models, the inventory cannot be carried over between periods. Let the true demand process given

$$\begin{array}{llll} D_{t} & = & {\alpha D_{t - 1} + \epsilon} & \\ \end{array}$$

where $D_{t}$ is the demand in period $t$, $\alpha \in \left\lbrack {0,1} \right)$ is a constant that is used to capture the autocorrelation between demands in two consequitive periods, and $\epsilon$ is normally distributed noise term with mean $\mu\left( {1 - \alpha} \right)$ and standard deviation $\sigma\sqrt{1 - \alpha^{2}}$. The (possibly unusual) parametrization of the error term ensures that irrespective of the value of $\alpha$, the unconditional distribution for every $D_{T}$ (for $T$ sufficiently large) is independent of $\alpha$; specifically, this unconditional distribution is distributed normally with mean $\mu$ and standard deviation $\sigma.$

Optimal Decisions & Demand-Chasing

With this setup, which is the canonical newsvendor model with the exception of an autocorrelated demand process, the conditional distribution of $D_{t - 1}$ is normal with mean $\alpha D_{t - 1} + \mu\left( {1 - \alpha} \right)$ and standard deviation $\sigma\sqrt{1 - \alpha^{2}}$. Hence, the optimal order quantity is given by

$$\begin{array}{llll} Q_{t}^{*} & = & {\alpha D_{t - 1} + \mu\left( {1 - \alpha} \right) + \sigma\sqrt{1 - \alpha^{2}}\Phi^{- 1}\left( \frac{p - c}{p} \right)} & \\ \end{array}$$

where $\Phi^{- 1}\left( . \right)$ is the inverse cumulative standard normal distribution.

As can be observed, when the demand process is autocorrelated, the manager should optimally adjust her ordering quantity based on previous periods demand. More importantly, when $\alpha > 0$, then order quantities will adjust upward when past period demand is higher, and the manager looks like she is chasing demand.

Suboptimal Newsvendors & Pure Demand-Chasing

In the model I proposed above, the true autocorrelation of demand is $\alpha$. In this section, I shall compare two types of decision-makers.

Newsvendors who are oblivious to the autocorrelation and assume that each period’s demand is independent of the next. That is, while the true $\alpha$ associated with the demand process may be non-zero, these decision-makers believe that $\alpha = 0$, and that $D_{t}$ is normally distributed with mean $\mu$ and standard deviation $\sigma$. Such a newsvendor should place order $Q_{t} = \mu + \sigma\Phi^{- 1}\left( \frac{p - c}{p} \right)$. Let the corresponding (long-run) expected per-period profit be $\Pi_{n}\left( \alpha \right)$.
Managers who are pure demand chasers; i.e., their order quantity in each period $t$ is $Q_{t} = Q_{t - 1} + \beta\left( {D_{t - 1} - Q_{t - 1}} \right)$. Let the corresponding (long-run) expected per-period profits be $\Pi_{c}\left( \alpha \right).$

Needless to say, the demand-chasing ordering rule is very conservative in that it does not even allow these managers to adjust their order quantity based on the prices or the margins. Specifically, this heuristic rule, one may expect, handicaps the demand-chasers as much as possible relative to the newsvendor who does not believe that the demand is autocorrelated. Despite this, is it always the case that the newsvendor who is oblivious to the autocorrelation makes more profits relative to the pure demand-chaser, i.e., is $\Pi_{c}\left( \alpha \right) - \Pi_{n}\left( \alpha \right) < 0$ ?

Given the complexity of obtaining closed-form solutions for the profits (especially with normal distributions), I employed numerical simulations to characterize the change in $\Pi_{c}\left( \alpha \right) - \Pi_{n}\left( \alpha \right)$ as a function of true demand auto-correlation$\alpha$. Figure below shows this curve. As may be observed, unless the true $\alpha$ is very low, the pure-demand chaser will perform better relative to the newsvendor who assumes no autocorrelation. Indeed, additional simulations where I examined demand-chasers who accounts for margins and prices (and thus adjusts it suboptimally toward the newsvendor quantity) performs even better and reduces the range of autocorrelations for which the newsvendor performs better. It appears that when a manager is facing a realistic demand process (where the autocorrelations may be unknown), demand-chasing (even if it disregards the newsvendor quantities) performs better compared to the optimal newsvendor who disregards autocorrelation. Thus, if we are to accept that the manager, in her ecology, is likely to encounter autocorrelated demand processes, then my results demonstrate that demand-chasing is not a bug, but is a feature, and is in fact ecologically rational.

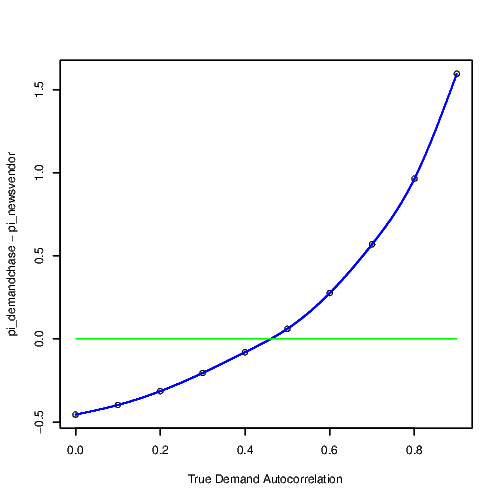
The figure was plotted for $\mu = 5,\sigma = 1,c = 6,p = 10,\beta = 0.3$

Figure 1: Profits from demand chasing minus from “optimal” newsvendor