If you cannot win the game, change the rules

Posted on Wed 01 November 2017 in Innovation, NPD

One of my wonderful coauthors mistaking me for someone who watches sports, shared some “sports” sayings with me. One of these was the profound sounding but somewhat meaningless (at least to me) saying about changing the rules if you can’t win. Anyway, given that I am interested in economic contests, I thought it might be fun to lay out a model for when and why changing the rules might be a good idea. As always, anything good in the model is because of my collaborators, and any errors are my own.

When matched against better positioned competitor, it might prove difficult to win. In such competitions, one approach to evening the odds might be to engage in sabotage where a person not only works to improve their performance, but also to decrease their competitors performance. For a survey of related literature, see Chowdhury & Gurtler, 2015.

An alternative approach might be to take actions to change the game altogher. For instance, if I am matched against Stephen Curry in a free throw contest, the odds that I win are vanishingly small. But maybe if I can change the game to also include that the players wear blindfolds, then, maybe I can improve my odds slightly (?). Or consider the more practical (and definitely more boring) thought experiment - suppose a startup is competing against a large company. If the startup decides to offer the product for free, and chooses to monetize its customer base through some other business model, this changes the rules of the game. Specifically, such an action possibly changes the customer perceptions, in turn changing the marginal return from existing competencies that the status-quo firm has. In this reshuffled market, the winner changes from whoever had greater competencies along the status-quo dimension, to one where some new competitive dimension becomes the measure that determines the winner. Thus, in this new game the existing status-quo company might have no real advantage compared to the new startup.

This short note will attempt to offer an economic analysis of the “change the rules” by viewing changing the rules as formally equivalent to changing the marginal value of ALL the players actions equally. So loosely speaking, this strategy is similar to sabotaging the opponent and sabotaging oneself.

To make the setting concrete, let us consider a setting that I faced recently while teaching a course, and I had a decide on what type of final exam to set Specifically, the “degree of difficulty” of the final exam is a variable under my control. With a tough exam, the marginal improvement in the final exam score for each unit increase in effort (prep time) be lower. In contrast, with an easy exam, the marginal improvement in a student’s score for each unit increase in effort (prep time) would be higher.

To build a formal model, let us assume that there are only two students, and both have already written the midterm exam. One of them scored $0.5$ and the other scored $0$ in the midterm. Just for fun, let us call the student who scored higher the “topdog” (or T) and the student who scored lower the “underdog” (or U).

In my course, the final grades are determined by the sum of midterm scores and final scores. Moreover, assume that the I am going to use a relative grading scheme, where whoever has the higher cumulative score gets an A, and the other student gets a B.

Assume that when a student puts in effort $e$ to prepare for the final exam, it costs her $e^{2}$, and let the probability that she gets a final exam score of $1$ is $\frac{e}{D}$, and with the remaining probability she gets a score of $0$.

We shall interpret the parameter $D$ as the difficulty of the final exam. Note that as $D$ increase, the probability that a student gets $1$ in final exam (for the same effort) decreases. So this interpretation is at least defensible. Thus, “changing the rules,” in this interpretation, is the same as increasing $D$, effectively making performance more difficult to attain for everyone.

Finally, to set up the students utility functions (and choices), assume that the students (identically) value an A grade at 1, and a B grade at 0. Then, the topdogs utility from putting in effort $e_{T}$ when the underdog puts in effort $e_{U}$ is given by

$$\pi _{T}=\frac{e_{T}}{D}+\left( 1-\frac{e_{T}}{D}\right) \left( 1-\frac{e_{U}}{D}\right) -e_{T}^{2}$$

and the underdogs utility is given by

$$\pi _{U}=\frac{e_{U}}{D}\left( 1-\frac{e_{T}}{D}\right) -e_{U}^{2}$$

Straightforward differentiation verifies that the best response for topdog is given by $e_{T}\left( e_{U}\right) =\frac{e_{U}}{2D^{2}}$, and the best response for underdog is given by $e_{U}\left( e_{T}\right) =\frac{\left( D-e_{T}\right) }{2D^{2}}$

Thus, the Nash equilibrium effort’s are given by

$$e_{T}^{\ast }=\left( \frac{D}{4D^{4}+1}\right)$$

$$e_{U}^{\ast }=\left( \frac{2D^{3}}{4D^{4}+1}\right)$$

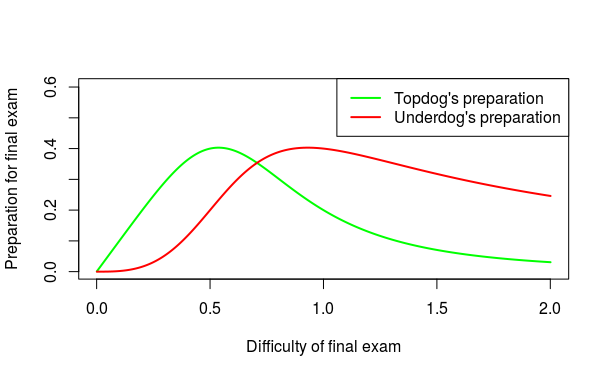
The plot below shows the equilibrium effort as a function of final exam difficulty. It is interesting to observe that the underdog puts in more (less) effort when the exam is more difficult.

The expected final exam score (in equilibrium) is shown in the plot below.

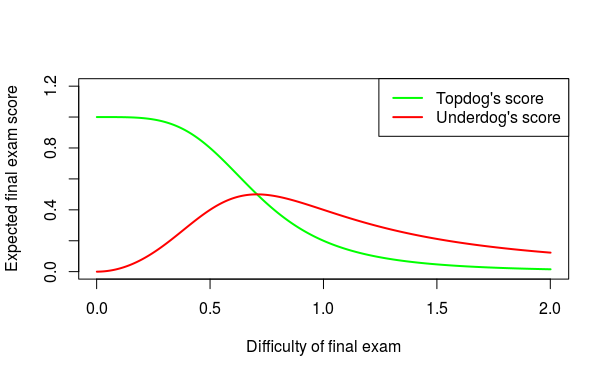
If, as a faculty, my goal is to maximize the total effort that the class puts into the final exam preparation (i.e., maximize $e_T + e_U$), then I will set the difficulty at $D=\frac{1}{\sqrt{2}}.$

If, on the other hand, I want to maximize the average final exam score, I will set the difficulty at $D=\frac{1}{2}\sqrt{2}\sqrt{\sqrt{2}-1}.$

Either way, it is interesting that there is an optimal difficulty level that maximizes effort and/or scores. So I should not set too easy or too difficult an exam.

It is also instructive to look at the payoffs to the underdog and topdog in the equilibrium

$$\pi _{T}^{\ast }=\frac{16D^{8}-8D^{6}+8D^{4}-D^{2}+1}{\left( 4D^{4}+1\right) ^{2}}$$

$$\pi _{U}^{\ast }=\frac{4D^{6}}{\left( 4D^{4}+1\right) ^{2}}$$

The plot below shows the equilibrium payoffs for the students. Interestingly, underdog prefers to write a moderately difficult final exam (specifically, $D=\frac{\root{4}\of{3}}{\sqrt{2}}$ gives the highest payoff to the underdog). However, the topdog prefers a super-easy exam (or a super-difficult one).

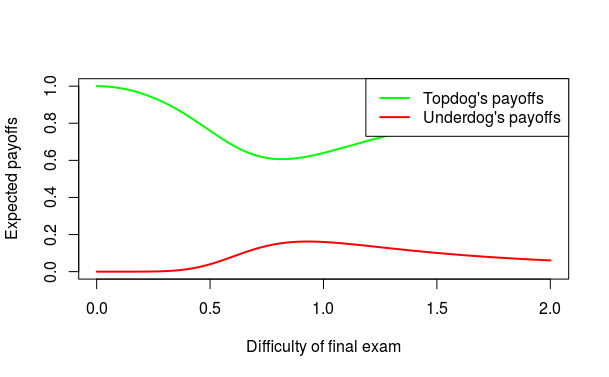
The main insight that we were trying to obtain, why does it make sense for a person (underdog) to try to change the rules of the game, comes through nicely in the plot above. Specifically, the underdog would change the rules of the game moderately - not too much, not too little - to ensure she can even odds in the resulting contest. In fact, from the social perspective, this is good (since this increases the individual effort levels).

It would be interesting to parametrize other factors (like the benefit of coming first, cost structure, etc) to see how much the entrant might attempt to change the rules. But that is left as an exercise for the reader :)