On last digit of prices
Posted on Mon 22 April 2013 in Random Thoughts
I had obtained data on the prices and the popularity rank of some 600 odd products from Flipkart.com website for a different project. Given that I had this data, it seemed like an interesting experiment to see if conventional wisdom that marketers like to have prices end in ‘9’ was true. The products I collected were in 3 distinct product categories (200 in each of the following categories - cellphones, cameras, and laptops), and included 38 distinct brands. After checking with flipkart, it was confirmed that the popularity rank was determined by sales. This suggests that it might be reasonable to interpret the rank as proxying demand. Hence, we define demand as \(\left(200-\mbox{popularity}\right)\).
The regressions shown below were conducted to examine the role of the last digit of the prices.
| Dependent variable: | |||
| Demand (200-Ranking) | |||
| (1) | (2) | (3) | |
| Category | No | No | Yes |
| Brand | No | No | Yes |
| Category:Price | No | No | Yes |
| Brand:Price | No | No | Yes |
| Price | -0.00047** | -0.00053** | 0.00073 |
| (0.00023) | (0.00023) | (0.00483) | |
| Last Digit | 2.59484*** | 2.51918*** | |
| (0.59925) | (0.63517) | ||
| Observations | 600 | 600 | 600 |
| R2 | 0.18112 | 0.20775 | 0.24303 |
| Adjusted R2 | 0.12253 | 0.14953 | 0.13961 |
| Residual Std. Error | 54.12687 (df = 559) | 53.28744 (df = 558) | 53.59736 (df = 527) |
| F Statistic | 3.09106*** (df = 40; 559) | 3.56876*** (df = 41; 558) | 2.34996*** (df = 72; 527) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 | ||
The data shows that on average when the price decreases by one unit from a round number price to a 9-ending price, the sales ranking improves by \(2.59\times9+0.0005\approx23\). So the last digit does have the predicted effect of improving the sales.
Given that this bias seem to be fairly well-known, even to the proverbial man on the street, does the data show any evidence that not all last digit manipulations can work as well?
To check this, we conduct a regression to look for the interaction of last digit and second last digit. Specifically, we look to see if the last digit effect is stronger for prices like 29 as opposed to prices like 99. A positive finding could be consistent with people discounting the last digit as soon as the prices seem too much like they are being manipulated.
| Dependent variable: | ||
| Demand (200-Ranking) | ||
| (1) | (2) | |
| Category | Yes | Yes |
| Brand | Yes | Yes |
| Category:Price | Yes | Yes |
| Brand:Price | Yes | Yes |
| Last Digit (D1) | 2.53801*** | 6.64967*** |
| (0.68015) | (1.63278) | |
| 2nd Last Digit (D2) | -0.05745 | 1.08378 |
| (0.73750) | (0.84101) | |
| Interaction (D1:D2) | -0.58192*** | |
| (0.21036) | ||
| Observations | 600 | 600 |
| R2 | 0.24304 | 0.25391 |
| Adjusted R2 | 0.13799 | 0.14875 |
| Residual Std. Error | 53.64798 (df = 526) | 53.31190 (df = 525) |
| F Statistic | 2.31348*** (df = 73; 526) | 2.41450*** (df = 74; 525) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 | |
As the table illustrates, the interaction is significant. The figure below illustrates the interaction graphically.
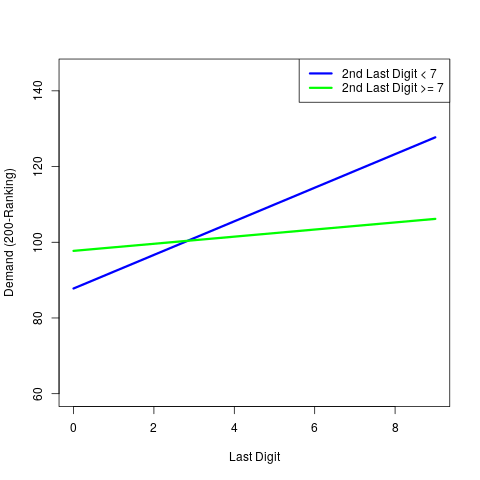
Thus, the last digit effect is more important when the second-last digit is small compared to when it is large (i.e., last digit effect is stronger when the price is 29 compared to when it is 99)!