Tullock Contests with Heterogeneous Outside Options

Posted on Sun 05 November 2017 in Innovation, NPD

I have been talking to some fellow academics for quite some time now about writing a paper that looks at contests and competition between contests. While that idea is still germinating, it did spawn an interesting thought about how to model stochastic participation in contests, one possibility I have documented below just in case I find time in the future to pursue it. As always, anything good with the model came from my collaborators, and all the errors are my own.

A Tullock contest is a useful way to model the idea of rent-seeking. The existing literature provides insight into how the parameters of the model, specifially, the prizes, the extent of competition, and the cost structure determines the intensive margin (the effort that each contest participant puts in). But less is known about the extensive margin (i.e., the choice of whether or not to participate in the contest). One category of models that has examined the extensive margin looks at the players who have an outside option (see for instance, Grossman & Dietl, 2015). In this short note, I shall try to expand on this idea by considering agents with heterogeneous outside options, and try to characterize both the intensive and extensive margins.

Consider $n+1$ players in a typical Tullock contest. Assume that each of these players have an outside option which is uniformly distributed in $\left[0,1\right]$. Note that this outside option value is private information.

To derive the equilibrium, let us first assume that in the equilibrium, a person enters the contest iff her outside option is below a threshold $p$. That is, any player has a probability $p$ of entering the contest.

The utility for player $1$ when he exerts effort $e$ and everyone else exerts effort $E$ is given by

$$ V\left(\sum_{i=0}^{n}{n \choose i}p^{i}\left(1-p\right)^{n-i}\left(1-\frac{iE}{e+iE}\right)\right)-e $$

Hence, the equilibrium effort can be found by straightforward first-order conditions as

$$ e=V\left(\sum_{i=0}^{n}{n \choose i}p^{i}\left(1-p\right)^{n-i}\left(\frac{i}{\left(i+1\right)^{2}}\right)\right) $$

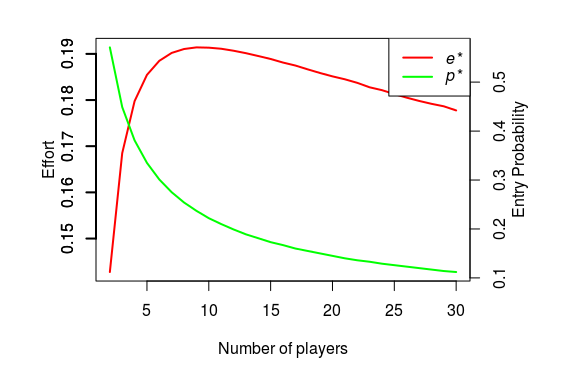
Thus, in (a rational expectations) equilibrium, threshold is $p^{\ast}$ where $p^{\ast}$ is the solution of

$$ V\left(\sum_{i=0}^{n}{n \choose i}p^{i}\left(1-p\right)^{n-i}\left(\frac{1}{i+1}\right)\right)-V\left(\sum_{i=0}^{n}{n \choose i}p^{i}\left(1-p\right)^{n-i}\left(\frac{i}{\left(i+1\right)^{2}}\right)\right)=p $$

and the equilibrium effort (accounting for entry) is given by

$$ e^{\ast}=V\left(\sum_{i=0}^{n}{n \choose i}\left(p^{\ast}\right)^{i}\left(1-p^{\ast}\right)^{n-i}\left(\frac{i}{\left(i+1\right)^{2}}\right)\right) $$

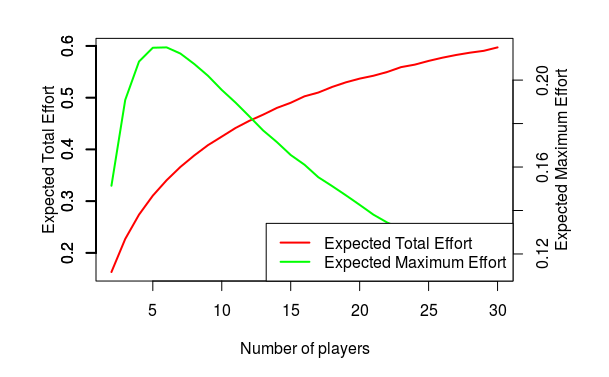
The expected total effort is $\left(n+1\right)p^{\ast}e^{\ast}$, and the expected maximum effort is $\left(1-\left(1-p^{\ast}\right)^{n+1}\right)e^{\ast}$.

Conditional on entering the contest, it is interesting that the effort is non-monotone in the number players. And the probability of participation (for a given player) decreases with the number of players.

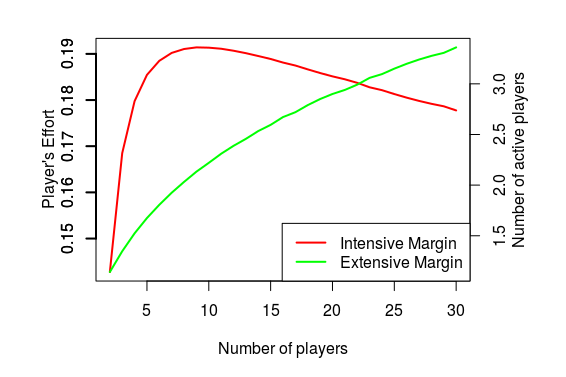
The figure below shows that the extensive margin (i.e., the expected number of players who put in non-zero effort) goes up with $n$. But the intensive margin (i.e., the effort exerted by the participating players) is non-monotone in $n$, and there is an intermediate value that maximizes the active participant’s effort.

The figure below shows that the firm will choose to have large participant pool if the goal is to maximize the total effort. However, if the goal is to maximize the expected maximum effort, then the firm has an “optimal size” for the tullock contest.