Do we search more with parallel search or with sequential search?

In their study examining the tradeoffs between parallel and sequential testing, Loch et al (2001) highlight a rather curious conclusion: sequential testing, because of its ability learn from one to next, will result in fewer tests. Indeed, the ability to learn from one to next can enable faster stopping (and thus fewer tests), but it does not seem so intuitive that the ability to learn can only have a one-sided effect. Specifically, can it be that sequential testing results in greater number of tests?

Below a simple model that helps reason about this question - when is it possible that optimal sequential testing leads to more tests compared to optimal parallel testing.

Follow the traditional formulation of the pandora’s box model (a la Weitzman) where an agent who sequentially engages in costly search with the goal of selecting a single best alternative. In the model, the agent makes the choice between continued search and termination dynamically, depending on the values that have been revealed so far. In contrast to the sequential search model, a parallel search model assumes that all the search is done concurrently and views the number of alternatives to examine as the relevant decision that is ex-ante committed to.

To make things concrete, assume that we have infinite number of possible alternatives that we can examine. Furthermore, suppose that these alternatives have value that are uniformly distributed between \(0\) and \(1\). Finally, let the cost of examining each alternative be \(c\).

With parallel search, if we look at \(n\) alternatives, then the expected value we obtain is the expected value of the maximum of \(n\) random distributed variables, each uniformly distributed between \(0\) and \(1\). We may show that this is exactly equal to \(\frac{n}{n+1}\). Thus, netting out the cost, we obtain that the net profit from searching \(n\) alternatives as \(\frac{n}{n+1}-nc\). Maximizing the net profits, we obtain the optimal number of alternatives that the agent should look at is \(n_{p}^{\ast}=\frac{1}{\sqrt{c}}-1\).

With sequential search, the optimal policy is a reservation price policy where the agent continues searching as long as the highest value so far is below \(R\) where \(R\) solves the equation \(R^{2}+\left(1-R\right)\frac{1+R}{2}-R=c\). Note that this is a straightforward application of Weitzman’s results. Thus, \(R=1-\sqrt{2c}\). The probability that the agent will search one more is the probability that the current searched value is less than \(R\), which because of our assumption of uniform distribution is exactly equal to \(R\). Hence, the probability that the agent searches 1 or more alternatives is \(1\), that they search 2 or more alternatives is \(R\), that they search 3 or more alternatives is \(R^{2}\), and so on. Thus, the expected number of alternatives that the agent searches is given by \(1+R+R^{2}+\cdots=\frac{1}{1-R}=\frac{1}{\sqrt{2c}}\).

From the above, we obtain that the agent will search more under sequential compared to parallel iff \(\frac{1}{\sqrt{2c}}>\frac{1}{\sqrt{c}}-1\). That is, \(c>\left(1-\frac{1}{\sqrt{2}}\right)^{2}\approx0.09\). So when cost is low, parallel testing ends up testing more alternatives whereas when the cost is higher, then sequential testing would end up testing more alternatives.

Note1: The revenue from parallel testing is \(1-\sqrt{c}\); and from sequential is \(1-\sqrt{\frac{c}{2}}\). So the revenue from sequential is always larger than the revenue from parallel.

Note2: The relevant range of \(c\) is \((0,\frac{1}{4})\), because beyond \(c=\frac{1}{4}\), the optimal number in the case of parallel is less than 1 (which is logically inconsistent).

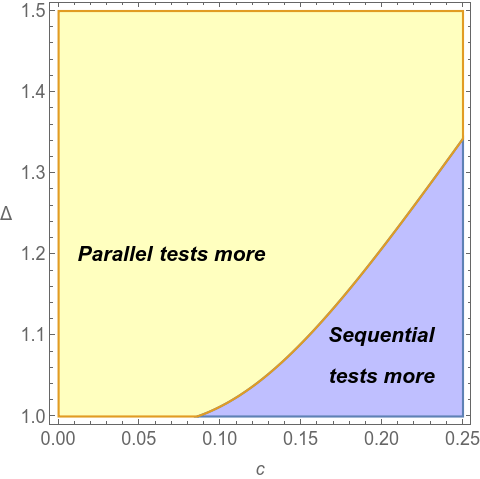
Note3: The model assumed that alternatives are uniformly distributed between \(0\) and \(1\). In case the alternatives are uniformly distributed between \(\mu-\frac{\Delta}{2}\) and \(\mu+\frac{\Delta}{2}\), then \(n_{s}^{\ast}=\frac{2}{\sqrt{8c\Delta+9\Delta^{2}-10\Delta+1}-3\Delta+3}\) and \(n_{p}^{\ast}=\sqrt{\frac{\Delta}{c}}-1\). As may be observed from the figure, when uncertainty is high and/or when the cost is low, parallel testing involves testing more alternatives. In contrast, when uncertainty is low and/or when cost is high, then sequential testing involves testing more alternatives.