How many people should I ask for advice (part 2)?

Posted on Sat 02 December 2023 in Research

The earlier musings calculated the expected value under the assumption that we need to decide how many people to ask upfront. Now suppose we can ask people sequentially. That is, we ask one person, and depending on their report can decide to stop or to ask more people, and so on. What should our optimal look for advisors policy be?

The model is similar to before, with the difference that after asking each person, we can update the prior. After the $n$ people have made their reports, we will revise our expectation of the alternatives true value to

$$\hat{\mu}_{n}=\mu+\sum_{i=1}^{n}\left(\frac{\sigma^{2}}{n\sigma^{2}+\frac{1}{\tau^{2}}}\right)\left(m_{i}-\mu\right)$$

which may be recursively written as

$$\begin{aligned} \mu_{n} & = & \mu_{n-1}+\frac{\sigma^{2}}{n\sigma^{2}+\frac{1}{\tau^{2}}}\left(m_{n}-\mu_{n-1}\right) \end{aligned}$$

Thus,

$$\begin{aligned} \mu_{n} & \sim & \mu_{n-1}+\frac{\sigma^{2}}{n\sigma^{2}+\frac{1}{\tau^{2}}}\left(\mathbf{m_{n}}-\mu_{n-1}\right) \end{aligned}$$

We may show that $\mathbf{m_{n}}$ is normally distributed with mean $\mu_{n-1}$ and variance $\sigma^{2}+\frac{1}{\tau^{2}}-\frac{\left(n-1\right)\sigma^{2}}{\left(n-1\right)\sigma^{2}+\frac{1}{\tau^{2}}}=\frac{n\sigma^{2}\tau^{2}+1}{(n-1)\sigma^{2}\tau^{4}+\tau^{2}}$. Thus,

$$\begin{aligned} \mu_{n} & \sim & \mu_{n-1}+\frac{\sigma^{2}\tau^{2}}{n\sigma^{2}\tau^{2}+1}\sqrt{\frac{n\sigma^{2}\tau^{2}+1}{(n-1)\sigma^{2}\tau^{4}+\tau^{2}}}\mathbf{Z}\\ & \sim & \mu_{n-1}+\frac{\sigma^{2}\tau}{n\sigma^{2}\tau^{2}+1}\sqrt{\frac{n\sigma^{2}\tau^{2}+1}{(n-1)\sigma^{2}\tau^{2}+1}}\mathbf{Z} \end{aligned}$$

So either you obtain $\mu_{n-1}^{+}$ if we stop, or we obtain $E\left[\left(\mu_{n-1}+\frac{\sigma^{2}\tau}{n\sigma^{2}\tau^{2}+1}\sqrt{\frac{n\sigma^{2}\tau^{2}+1}{(n-1)\sigma^{2}\tau^{2}+1}}\mathbf{Z}\right)^{+}\right]-c$ if we ask one more person.

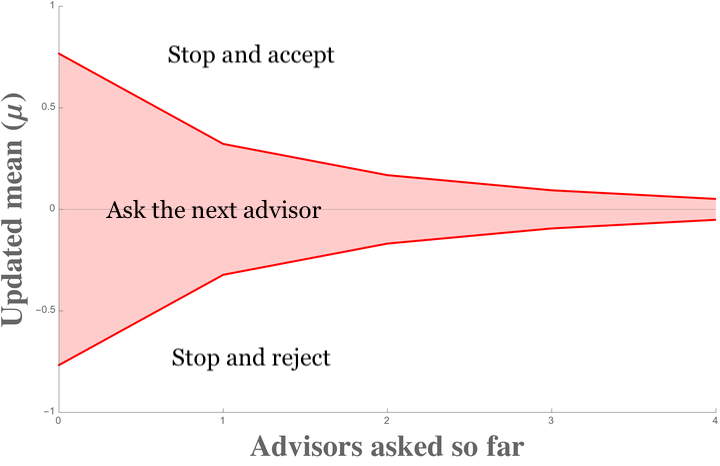
From the above, we should be able to compute the stopping thresholds $R_{n}$ and $-R_{n}$if $\mu_{n}>R_{n}$, we stop and accept; and if $\mu_{n}<-R_{n}$, we stop and reject. If $\mu_{n}\in\left[-R_{n},R_{n}\right]$, then we continue asking the next advisor for their opinion. It is interesting to note that this result is similar in flavor to the classic Lippman & McCardle (1991).

::: center :::