How many people should I ask for advice (part 3)?

Posted on Thu 07 December 2023 in Research

The earlier model assumed that we wish to maximize the expected value from the decision (“impact”). What if we are interested in maximizing the probability that we are making the right decision. How would the optimal choice change? As before, after asking $n$ people, we will update the true value to $N\left(\mu_{n},\sigma_{n}\right)$ where

$$\begin{aligned} \mu_{n} & \sim & \mu+\sigma^{2}\sqrt{\frac{n}{n\sigma^{2}+\frac{1}{\tau^{2}}}}\mathbf{Z}\\ \sigma_{n} & = & \sigma^{2}\left(1-\sqrt{\frac{n\sigma^{2}}{n\sigma^{2}+\frac{1}{\tau^{2}}}}\right) \end{aligned}$$

If $\mu_{n}>0$, we will choose to accept, and the probability of making the right choice is $\mu_{n}+\sigma_{n}\hat{\mathbf{Z}}>0$, i.e., $\hat{\mathbf{Z}}>-\frac{\mu_{n}}{\sigma_{n}}$, i.e., $1-\Phi\left(-\frac{\mu_{n}}{\sigma_{n}}\right)$. Alternatively, if $\mu_{n}<0$, we will choose to reject, and the probability of making the right choice is $\mu_{n}+\sigma_{n}\hat{\mathbf{Z}}<0$, i.e., $\hat{\mathbf{Z}}<-\frac{\mu_{n}}{\sigma_{n}}$, i.e., $\Phi\left(-\frac{\mu_{n}}{\sigma_{n}}\right)$. Note that if $\mu_{n}>0$, then $\Phi\left(-\frac{\mu_{n}}{\sigma_{n}}\right)<1-\Phi\left(-\frac{\mu_{n}}{\sigma_{n}}\right)$. Consequently, we may write down the expected probability that we make the right choice as

$$E\left[\max\left\{ \Phi\left(-\frac{\mu_{n}}{\sigma_{n}}\right),1-\Phi\left(-\frac{\mu_{n}}{\sigma_{n}}\right)\right\} \right]$$

Consider the case of $\mu=0$. Then,

$$\begin{aligned} \frac{\mu_{n}}{\sigma_{n}} & = & \frac{\sigma^{2}\sqrt{\frac{n}{n\sigma^{2}+\frac{1}{\tau^{2}}}}}{\sigma^{2}\left(1-\sqrt{\frac{n\sigma^{2}}{n\sigma^{2}+\frac{1}{\tau^{2}}}}\right)}\mathbf{Z}\\ & = & \frac{1}{\left(\sqrt{1+\frac{1}{n\sigma^{2}\tau^{2}}}-1\right)}\mathbf{Z} \end{aligned}$$

Consequently, the expected probability of making the right choice is

$$E\left[\Phi\left(\frac{1}{\sqrt{1+\frac{1}{n\sigma^{2}\tau^{2}}}-1}\mathbf{Z}\right)|\mathbf{Z}>0\right]$$

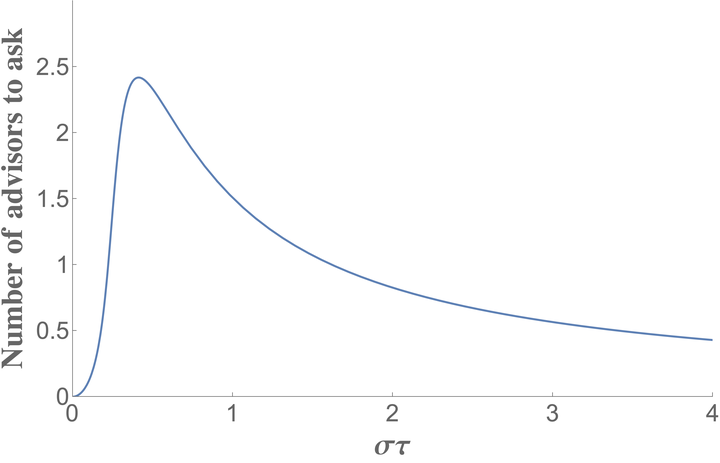
Consider the function $g\left(\theta\right)=E\left[\Phi\left(\theta\mathbf{Z}\right)|\mathbf{Z}>0\right]=1-\frac{\tan^{-1}\left(\frac{1}{\theta}\right)}{\pi}$; then we should maximize $1-\frac{\tan^{-1}\left(\sqrt{1+\frac{1}{n\sigma^{2}\tau^{2}}}-1\right)}{\pi}$ , i.e., minimize $\tan^{-1}\left(\sqrt{1+\frac{1}{n\sigma^{2}\tau^{2}}}-1\right)$ so as to obtain the highest probability of making the right choice (conditional on the cost of course). As an example, suppose the net payoffs is given by $1-\frac{\tan^{-1}\left(\sqrt{1+\frac{1}{n\sigma^{2}\tau^{2}}}-1\right)}{\pi}-cn$. Then, the dependence of optimal $n^{\ast}$ on $\sigma\tau$ is shown in the figure below.

As can be noted, we ask for advise from most people either the fidelity and uncertainty are both moderate. So if our objective was to minimize the probability of making an error, we will ask for fewer advisors when the ex-ante uncertainty of the alternative is very large!