How many people should I ask for advice?

Posted on Mon 27 November 2023 in Research

We like to ask for other’s opinions before embarking on any venture. Is there a way to understand the determinants of how many people should we ask for advice? Below is a “simple” model that might help think through the various drivers.

Suppose we have a single alternative that we want to decide whether to choose or to forgo. Our ex-ante belief is that the alternative has value that is distributed normally with mean $\mu$ and standard deviation $\sigma$. Obviously, if we have to rely on our ex-ante beliefs, they we should compare this ex-ante expectation against the value of forgoing it (assumed to be normalized to $0$). That is, we accept the alternative if $\mu>0$, and forgo it otherwise.

Now suppose that we can collect information about the alternative before we have to make the decision. Specifically, we can ask a person $i$ ($i=1,2,\cdots,n$) for their judgements of the true value of the alternative. We shall assume that we ask all these people in parallel (i.e., simultaneously). And after they make their reports, we then make the decision.

Model the person’s $i's$ report as $\mathbf{m}_{i}=\mathbf{x}+\epsilon_{i}$ where $\mathbf{x}$ is the true value and $\epsilon_{i}$ is the person specific idiosyncratic measurement noise. More specifically, assume that this noise is normally distributed with mean $0$ and standard deviation $\frac{1}{\tau}$. Note that $\tau$ represents the fidelity of measurement, with lower/higher values representing lower/higher fidelity.

After the $n$ people have made their reports, we will revise our expectation of the alternatives true value to $\mu+\sum\left(\frac{\sigma^{2}}{k\sigma^{2}+\frac{1}{\tau^{2}}}\right)\left(m_{i}-\mu\right)$. Thus, ex-ante, we will belief that our ex-post belief will be distributed as $\mu+\sum\left(\frac{\sigma^{2}}{k\sigma^{2}+\frac{1}{\tau^{2}}}\right)\left(\mathbf{m_{i}}-\mu\right)$, which has the same distribution as

$$\begin{aligned} & \sim & \mu+\sum\left(\frac{\sigma^{2}}{n\sigma^{2}+\frac{1}{\tau^{2}}}\right)\epsilon_{i}+\frac{n\sigma^{2}}{n\sigma^{2}+\frac{1}{\tau^{2}}}\left(\mathbf{x}-\mu\right)\\ & \sim & \mu+\left(\frac{\sigma^{2}}{n\sigma^{2}+\frac{1}{\tau^{2}}}\right)\frac{1}{\tau}\sum\mathbf{Z_{i}}+\frac{n\sigma^{2}}{n\sigma^{2}+\frac{1}{\tau^{2}}}\mathbf{\left(x-\mu\right)}\\ & \sim & \mu+\left(\frac{\sigma^{2}}{n\sigma^{2}+\frac{1}{\tau^{2}}}\right)\frac{1}{\tau}\sqrt{n}\mathbf{\hat{Z}}+\frac{n\sigma^{2}}{n\sigma^{2}+\frac{1}{\tau^{2}}}\mathbf{\left(x-\mu\right)}\\ & \sim & \mu+\left(\frac{\sigma^{2}}{n\sigma^{2}+\frac{1}{\tau^{2}}}\right)\frac{1}{\tau}\sqrt{n}\mathbf{\hat{Z}}+\frac{n\sigma^{2}}{n\sigma^{2}+\frac{1}{\tau^{2}}}\sigma\frac{\mathbf{\left(x-\mu\right)}}{\sigma}\\ & \sim & \mu+\left(\frac{\sigma^{2}}{n\sigma^{2}+\frac{1}{\tau^{2}}}\right)\frac{1}{\tau}\sqrt{n}\mathbf{\hat{Z}}+\frac{n\sigma^{2}}{n\sigma^{2}+\frac{1}{\tau^{2}}}\sigma\mathbf{\tilde{Z}}\\ & \sim & \mu+\left(\frac{\sigma^{2}}{n\sigma^{2}+\frac{1}{\tau^{2}}}\right)\left(\frac{1}{\tau}\sqrt{n}\mathbf{\hat{Z}}+n\sigma\mathbf{\tilde{Z}}\right)\\ & \sim & \mu+\sigma^{2}\sqrt{\frac{n}{n\sigma^{2}+\frac{1}{\tau^{2}}}}\mathbf{Z} \end{aligned}$$

where $\mathbf{Z}$ is the standard normal.

Thus, the expected value if we ask for reports from $n$ people is

$$E\left[\left(\mu+\sigma^{2}\sqrt{\frac{n}{n\sigma^{2}+\frac{1}{\tau^{2}}}}\mathbf{Z}\right)^{+}\right]$$

Assume that it cost $c$ to ask for each additional report. Then, the expected value from asking $n$ reports is

$$V=E\left[\left(\mu+\sigma^{2}\sqrt{\frac{n}{n\sigma^{2}+\frac{1}{\tau^{2}}}}\mathbf{Z}\right)^{+}\right]-cn$$

Suppose $\mu=0$. Then,

$$\begin{aligned} V & = & \sigma^{2}\sqrt{\frac{n}{n\sigma^{2}+\frac{1}{\tau^{2}}}}\frac{1}{\sqrt{2\pi}}-cn \end{aligned}$$

Easy comparitive statics shows that

Ask reports from more people if the mean $\mu$ is close to zero (not too high or too low).
Ask reports from more people if variance $\sigma$ is moderate (not too high or too low).
Ask reports from more people if the fidelity $\tau$ is moderate (not too high or too low).

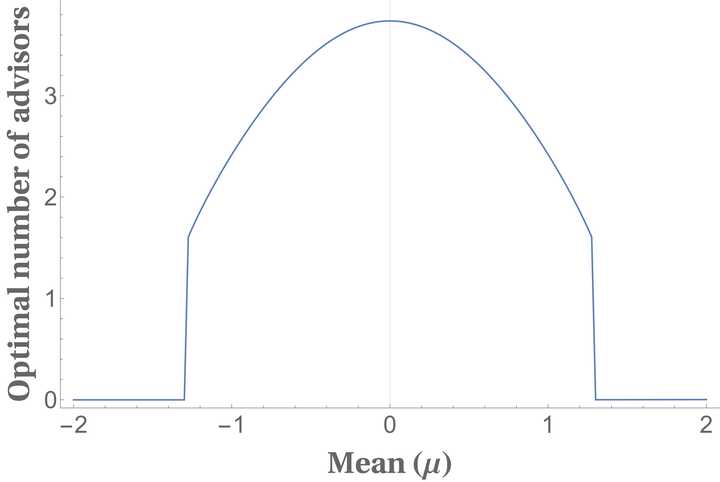
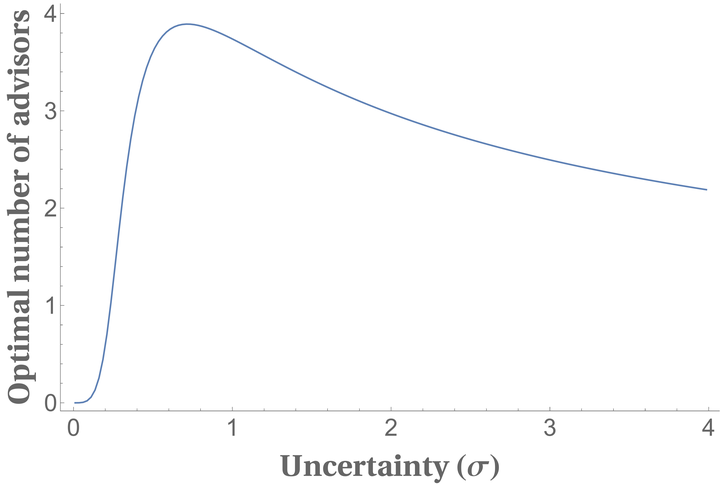
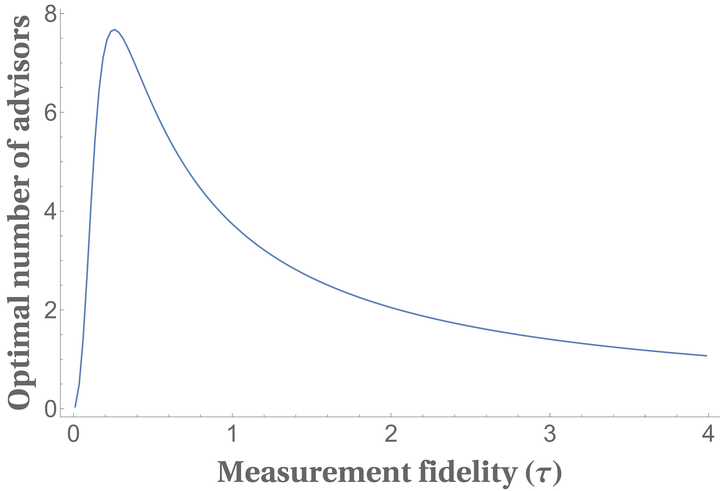
Asking one person versus asking many for advice

The model assumed that we ask $n$ people for their advice. One may imagine that a model where we ask exactly one person is less general. However, the following shows that these two are in fact equivalent in a technical sense. Specifically, the expected value after asking $n$ people, assuming that each person costs us $c$, is given by

$$E\left[\left(\mu+\sigma^{2}\sqrt{\frac{n}{n\sigma^{2}+\frac{1}{\tau^{2}}}}\mathbf{Z}\right)^{+}\right]-nc$$

Note that the above is identical to a setting where we ask exactly one person who has fidelity $\sqrt{n}\tau$ at cost $nc$!

Obviously, the equivalence still holds even when we optimize the number of advisors we request. Specifically, consider the setting where there is exactly one person with fidelity $\hat{\tau},$and whose cost is $c\left(\frac{\hat{\tau}}{\tau}\right)^{2}$. Then, if we are to maximize our payoff by modifying the fidelity, we obtain our maximal payoff as

$$\max_{\hat{\tau}}E\left[\left(\mu+\sigma^{2}\sqrt{\frac{1}{\sigma^{2}+\frac{1}{\hat{\tau}^{2}}}}\mathbf{Z}\right)^{+}\right]-c\left(\frac{\hat{\tau}}{\tau}\right)^{2}$$

Define $n=\left(\frac{\hat{\tau}}{\tau}\right)^{2}$. Then, the above maximal payoff is equivalent to

$$\max_{n}E\left[\left(\mu+\sigma^{2}\sqrt{\frac{n}{n\sigma^{2}+\frac{1}{\tau^{2}}}}\mathbf{Z}\right)^{+}\right]-nc$$

Consequently, if we can solve the optimal fidelity $\hat{\tau}^{\ast}$ in the case of a single advisor, we can easily obtain the optimal number of advisors for an arbitrary fixed fidelity as $n^{\ast}=\left(\frac{\hat{\tau}^{\ast}}{\tau}\right)^{2}$